Încălziți-vă pentru creier: puteți rezolva problema monedei contrafăcute? Verifică!

Matematicianul are doar trei încercări, deci nu puteți cântări fiecare monedă separat. Trebuie să le împărțiți în grămezi și să le puneți pe cântare mai multe bucăți odată, apropiindu-vă treptat de cea falsă.

Să presupunem că un matematician decide să împartă 12 monede în trei grămezi de câte patru monede fiecare. Apoi a pus patru monede pe fiecare cântar. Această cântărire poate da două rezultate. Să luăm în considerare fiecare dintre ele.

1. Greutatea celor două grămezi de monede era aceeași. Prin urmare, toți banii din ei sunt reali, iar contrafacerea se află undeva printre cele patru monede neponderate.

Pentru a urmări rezultatul, matematicianul marchează toate scripturile cu un zero. Apoi ia trei dintre ele și le compară cu trei monede neponderate. Dacă greutatea lor este egală, atunci restul (a patra) monedă neponderată este contrafăcută. Dacă greutatea este diferită, atunci matematicianul pune un plus pe cele trei monede nemarcate dacă sunt mai grele decât cele cu zerouri sau un minus dacă sunt mai ușoare.

Apoi ia două monedemarcat cu plus sau minus și compară greutatea acestora. Dacă este la fel, atunci copia rămasă este falsă. Dacă nu, matematicianul se uită la semne: printre monedele cu plus, falsul va fi cel mai greu, printre monedele cu minus, cel mai ușor.

2. Greutatea celor două grămezi de monede nu era aceeași.

În acest caz, matematicianul trebuie să acționeze astfel: marcați banii într-o grămadă grea cu un plus, într-o grămadă ușoară cu un minus, într-o grămadă neponderată cu un zero, deoarece se știe că copia falsă era pe cântar.

Acum trebuie să regrupați monedele pentru a vă menține în cele două cântăriri rămase. Una dintre modalități este de a lua în loc de trei monede cu un plus, trei monede cu un minus și de a pune trei piese cu un zero în locul lor.

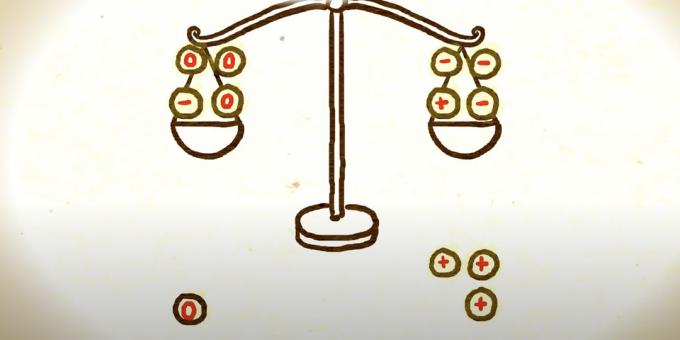
Urmează trei opțiuni posibile. Dacă scara care era mai grea depășește, atunci fie moneda veche cu semnul plus pe ea este mai grea decât celelalte, fie moneda cu semnul minus de pe cealaltă parte a cântarului este mai ușoară. Un matematician trebuie să aleagă oricare dintre ele și să se compare cu un model comun pentru a găsi un fals.

Dacă tava de cântărire, care era mai grea, a devenit mai ușoară, atunci una dintre cele trei monede cu semn minus mutat de matematician este cea mai ușoară. Acum trebuie să compare două dintre ele pe cântar. Dacă rezultatele sunt legate, a treia monedă va fi contrafăcută. În caz de inegalitate, cea falsă este mai ușoară.

Dacă bolurile sunt echilibrate după înlocuire, una dintre cele trei monede scoase de pe cântar cu semnul plus este mai grea decât celelalte. Un matematician trebuie să compare două dintre ele. Dacă sunt egali, al treilea este fals. Cu inegalitate, cel mai greu nu este real.

Împăratul dă din cap aprobator în timp ce ascultă raționamentul matematica, dar guvernatorul necinstit merge la închisoare.

Acest puzzle este o traducere a unui videoclip TED-Ed.